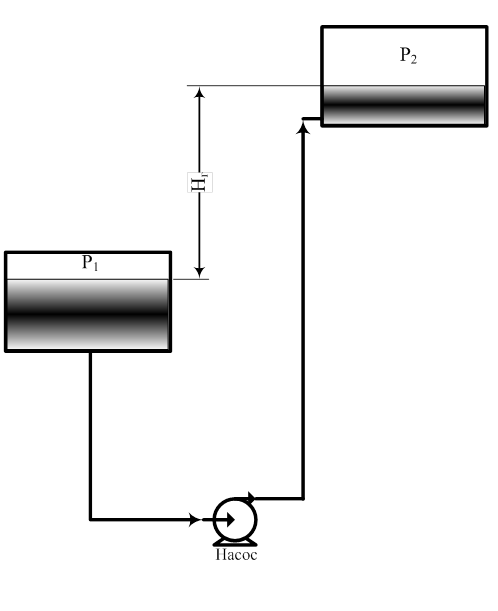
В теории гидродинамики доказывается, что напор (т.е. энергия!), который сообщает насос жидкости, расходуется в общем случае на три слагаемых (рис. 1):

Рис. 1. Принципиальная схема простейшей насосной установки

1. Жидкость надо поднять с уровня в первой ёмкости на уровень во второй ёмкости. Это так называемая геометрическая высота, её обозначают Н_г;

2. Насосу надо преодолеть разность давлений между емкостями, из которой он забирает жидкость (её так и называют – заборная ёмкость), и той, в которую он закачивает: .

3. На пути из ёмкости 1 в ёмкость 2 жидкость проходит какой-то путь, и на этом пути затрачивает энергию на преодоление сил собственного трения (эту величину так и называют – потери напора на трение) h_тр. И ещё жидкости приходится преодолевать всевозможные препятствия, которые мы на её пути поставили – повороты, расширения, сужения и т.д. Эту величину называют потери напора в местных сопротивлениях h_м.с.. Общая потеря напора будет равна

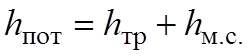
В итоге получается такая простая и красивая формула, в которой хорошо видны три названные слагаемые

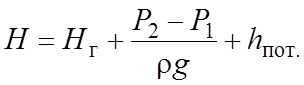
В этой формуле Н – напор (энергия!), который должен сообщить насос жидкости, чтобы она смогла дойти из одной точки в другую с заданным расходом Q.

Совершенно понятно, что расход жидкости Q может меняться. При этом будет меняться скорость потока. Так вот первые два слагаемых не зависят от скорости движения среды. А третья величина от скорости зависит, и очень сильно.

Ради упрощения пока пренебрежём величиной потери напора в местных сопротивлениях и сосредоточимся на потерях напора на преодоление сил трения – это главный наш «враг» при транспорте жидкостей по трубопроводам. В прикладной гидродинамике для расчётов величины широко используется ставшая классической формула Дарси-Вейсбаха

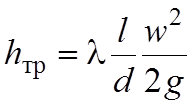
где l – длина трубопровода; м; d –диаметр трубы, м; w – скорость потока, м/с; λ – коэффициент трения, безразмерная величина; g – ускорение свободного падения, 9,81 м/с².

Величину коэффициента трения λ можно найти, если известен режим движения потока – ламинарный или турбулентный. А отличить один режим от другого можно по значению критерия (числа) Рейнольдса, который находится по формуле

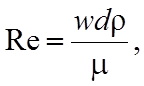
где ρ – плотность жидкости, кг/м³; μ – динамический коэффициент вязкости жидкости, Па×с.

Опытным путём установили, что если то режим движения будет ламинарным. Если же то режим движения турбулентный. А вот если то мы не знаем, какой режим будет. Этот диапазон значений критерия Рейнольдса назвали переходной областью.

Как правило, в технологических трубопроводах мы специально создаём турбулентный режим движения – при перекачивании он экономически выгоднее.

Так вот, для турбулентного режима коэффициент трения λ находится по формуле Блазиуса

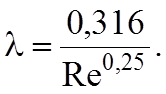
Эта формула получена путём обобщения огромного числа опытных данных, т.е. является эмпирической. Применима она только для гладких труб. Если труба старая и шероховатая, то расчёт коэффициента трения λ усложняется. Здесь я этот случай не рассматриваю. В контрольной работе вы будете рассчитывать новый трубопровод с гладкими трубами.

Перейдём к цели работы.